Find all the zeros of the polynomial $2 x^{3}+x^{2}-6 x-3$, if two of its zeros are $-\sqrt{3}$ and $\sqrt{3}$.
We know that if $x=\alpha$ is a zero of a polynomial, and then $x-\alpha$ is a factor of $f(x)$.
Since $\sqrt{3}$ and $-\sqrt{3}$ are zeros of $f(x)$.
Therefore
$(x+\sqrt{3})(x-\sqrt{3})=x^{2}-3$
$=x^{2}-3$
$x^{2}-3$ is a factor of $f(x)$.Now, we divide $2 x^{3}+x^{2}-6 x-3$ by $g(x)=x^{2}-3$ to find the other zeros of $f(x)$.
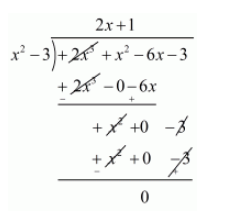
By using division algorithm we have $f(x)=g(x) \times q(x)-r(x)$
$2 x^{3}+x^{2}-6 x-3=\left(x^{2}-3\right) \times(2 x+1)+0$
$2 x^{3}+x^{2}-6 x-3=\left(x^{2}+\sqrt{3}\right)(x-\sqrt{3})(2 x+1)$
Hence, the zeros of the given polynomial are $-\sqrt{3},+\sqrt{3}, \frac{-1}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
