Find the area of a figure formed by joining the midpoints

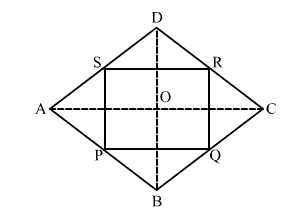
Let ABCD be a rhombus and P, Q, R and S be the midpoints of AB, BC, CD and DA, respectively. 
Join the diagonals, AC and BD.
In ∆ ABC, we have:

$P Q \| A C$ and $P Q=\frac{1}{2} A C$                 [By midpoint theorem]

$\mathrm{PQ}=\frac{1}{2} \times 16=8 \mathrm{~cm}$

Again, in ∆DAC, the points S and R are the midpoints of AD and DC, respectively.

$\therefore S R \| A C$ and $S R=\frac{1}{2} A C$         [By midpoint theorem]

$\mathrm{SR}=\frac{1}{2} \times 12=6 \mathrm{~cm}$

Area of PQRS $=$ length $\times$ breadth $=6 \times 8=48 \mathrm{~cm}^{2}$