Find the area of the region

The area bounded by the curves, $\left\{(x, y): y^{2} \leq 4 x, 4 x^{2}+4 y^{2} \leq 9\right\}$, is represented as

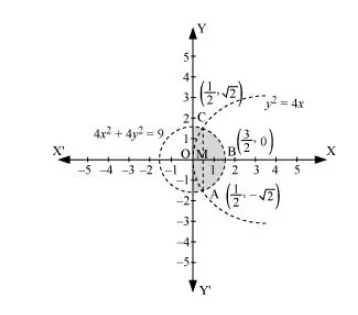
The points of intersection of both the curves are $\left(\frac{1}{2}, \sqrt{2}\right)$ and $\left(\frac{1}{2},-\sqrt{2}\right)$.

The required area is given by OABCO.

It can be observed that area OABCO is symmetrical about x-axis.

∴ Area OABCO = 2 × Area OBC

Area OBCO = Area OMC + Area MBC

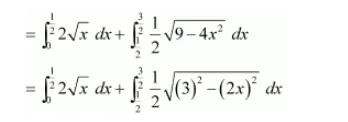
Put $2 x=t \Rightarrow d x=\frac{d t}{2}$

When $x=\frac{3}{2}, t=3$ and when $x=\frac{1}{2}, t=1$

$=\int_{0}^{\frac{1}{2}} 2 \sqrt{x} d x+\frac{1}{4} \int_{1}^{3} \sqrt{(3)^{2}-(t)^{2}} d t$

$=2\left[\frac{x^{\frac{3}{2}}}{\frac{3}{2}}\right]_{0}^{\frac{1}{2}}+\frac{1}{4}\left[\frac{t}{2} \sqrt{9-t^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{t}{3}\right)\right]_{1}^{3}$

$=2\left[\frac{2}{3}\left(\frac{1}{2}\right)^{\frac{3}{2}}\right]+\frac{1}{4}\left[\left\{\frac{3}{2} \sqrt{9-(3)^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{3}{3}\right)\right\}-\left\{\frac{1}{2} \sqrt{9-(1)^{2}}+\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right\}\right]$

$=\frac{2}{3 \sqrt{2}}+\frac{1}{4}\left[\left\{0+\frac{9}{2} \sin ^{-1}(1)\right\}-\left\{\frac{1}{2} \sqrt{8}+\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right\}\right]$

$=\frac{\sqrt{2}}{3}+\frac{1}{4}\left[\frac{9 \pi}{4}-\sqrt{2}-\frac{9}{2} \sin ^{-1}\left(\frac{1}{3}\right)\right]$

$=\frac{\sqrt{2}}{3}+\frac{9 \pi}{16}-\frac{\sqrt{2}}{4}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)$

$=\frac{9 \pi}{16}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{\sqrt{2}}{12}$

Therefore, the required area is $\left[2 \times\left(\frac{9 \pi}{16}-\frac{9}{8} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{\sqrt{2}}{12}\right)\right]=\frac{9 \pi}{8}-\frac{9}{4} \sin ^{-1}\left(\frac{1}{3}\right)+\frac{1}{3 \sqrt{2}}$ units