Question:
Find the domain and range of the function
$F: R \rightarrow R: f(x)=x^{2}+1$
Solution:
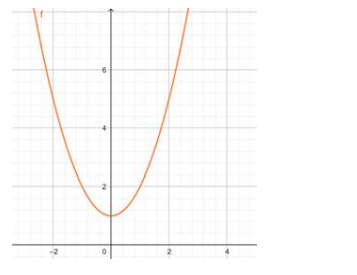
Since the function $f(x)$ can accept any values as per the given domain $R$, therefore, the domain of the function $f(x)=x^{2}+1$ is $R$.
The minimum value of $f(x)=1$
$\Rightarrow$ Range of $f(x)=[-1, \infty]$
i.e range $(f)=\{y \in R: y \geq 1\}$
Ans: dom $(f)=R$ and range $(f)=\{y \in R: y \geq 1\}$
