Find the equation of the line passing through the point (2, 3) and

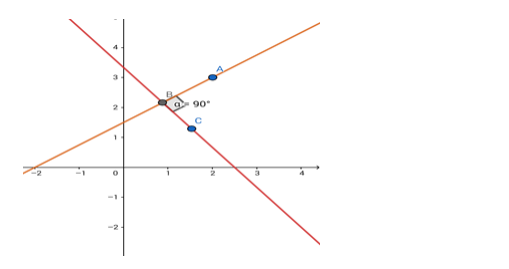
Given: The given line is $4 x+3 y=10$. The line perpendicular to this line passes through $(2,3)$.

Formula to be used: The product of slopes of two perpendicular lines = - 1

Slope of this line is $-4 / 3$.

$\therefore$ the slope of the perpendicular line $=\frac{-1}{-4 / 3}=3 / 4$.

The equation of the line can be written in the form $y=\left(\frac{3}{4}\right) x+c$

(c is the y - intercept)

This line passes through (2,3), so the point will satisfy the equation of the line.

$\therefore 3=\left(\frac{3}{4}\right) \times 2+$ ci.e.c $=3-\frac{3}{2}=\frac{3}{2}$

The required equation is

$y=\frac{3}{4} x+\frac{3}{2}$

or, 4y = 3x + 6 i.e. 3x - 4y + 6 = 0.