Find the length of each side of a rhombus whose diagonals are 24 cm and 10 cm long.

Let ABCD be the rhombus with diagonals (AC = 24 cm and BD = 10 cm) meeting at O.
We know that the diagonals of a rhombus bisect each other at right angles.
Applying Pythagoras theorem in right-angled triangle AOB, we get:

$A B^{2}=A O^{2}+B O^{2}=12^{2}+5^{2}$

$A B^{2}=144+25=169$

$A B=\sqrt{169}=13 \mathrm{~cm}$

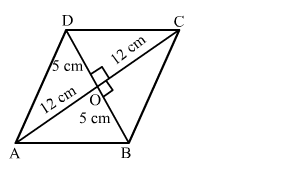
Hence, the length of each side of the rhombus is 13 cm.