Find the mean number of heads in three tosses of a fair coin.

Let X denote the success of getting heads.

Therefore, the sample space is

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

It can be seen that X can take the value of 0, 1, 2, or 3.

$\therefore \mathrm{P}(\mathrm{X}=0)=\mathrm{P}(\mathrm{TTT})$

$=\mathrm{P}(\mathrm{T}) \cdot \mathrm{P}(\mathrm{T}) \cdot \mathrm{P}(\mathrm{T})$

$=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$

$=\frac{1}{8}$

$\therefore P(X=1)=P(H H T)+P(H T H)+P(T H H)$

$=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$

$=\frac{3}{8}$

$\therefore \mathrm{P}(\mathrm{X}=2)=\mathrm{P}(\mathrm{HHT})+\mathrm{P}(\mathrm{HTH})+\mathrm{P}(\mathrm{THH})$

$=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}+\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$

$=\frac{3}{8}$

$\therefore \mathrm{P}(\mathrm{X}=3)=\mathrm{P}(\mathrm{HHH})$

$=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$

$=\frac{1}{8}$

Therefore, the required probability distribution is as follows.

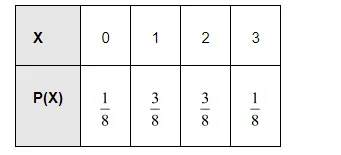
Mean of $X E(X), \mu=\sum X_{i} P\left(X_{i}\right)$

$=0 \times \frac{1}{8}+1 \times \frac{3}{8}+2 \times \frac{3}{8}+3 \times \frac{1}{8}$

$=\frac{3}{8}+\frac{3}{4}+\frac{3}{8}$

$=\frac{3}{2}$

$=1.5$