Find the mode of the following distribution.

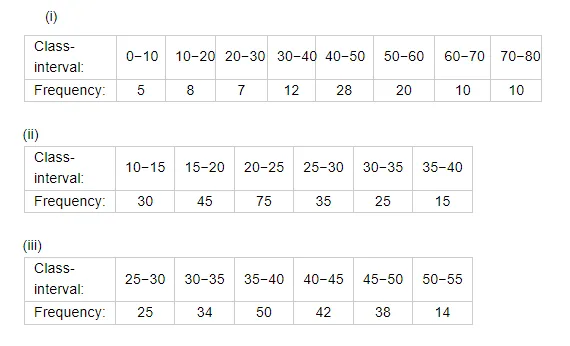
(i) Here, maximum frequency is 28 so the modal class is 40−50.

Therefore,

$l=40$

$h=10$

$f=28$

$f_{1}=12$

$f_{2}=20$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f+f_{1}-f_{2}} \times h$

$=40+\frac{28-12}{2 \times 28-12-20} \times 10$

$=40+\frac{16}{24} \times 10$

$=40+\frac{80}{12}$

$=40+6.67$

Mode $=46.67$

(ii) Here, maximum frequency is 75 so the modal class is 20−25.

Therefore,

$l=20$,

$h=5$

$f=75$

$f_{1}=45$

$f_{2}=35$

$\Rightarrow$ Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=20+\frac{75-45}{150-45-35} \times 5$

$=20+\frac{30}{70} \times 5$

$=20+\frac{30}{14}$

$=20+2.14$

Mode $=22.14$

(iii) Here, maximum frequency is 50 so the modal class is 35−40.

Therefore,

$l=35$

$h=5$

$f=50$

$f_{1}=34$

$f_{2}=42$

Mode $=l+\frac{f-f_{1}}{2 f-f_{1}-f_{2}} \times h$

$=35+\frac{50-34}{100-34-42} \times 5$

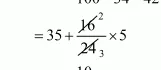
$=35+\frac{10}{3}$

$=35+3.33$

Mode $=38.33$