For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained.
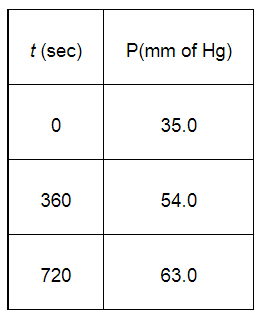
Calculate the rate constant.
The decomposition of azoisopropane to hexane and nitrogen at 543 K is represented by the following equation.

After time, $t$, total pressure, $\mathrm{P}_{t}=\left(\mathrm{P}_{0}-p\right)+p+p$
$\Rightarrow \mathrm{P}_{t}=\mathrm{P}_{0}+p$
$\Rightarrow p=\mathrm{P}_{\mathrm{t}}-\mathrm{P}_{0}$
Therefore, $\mathrm{P}_{\mathrm{o}}-p=\mathrm{P}_{\mathrm{o}}-\left(\mathrm{P}_{\mathrm{t}}-\mathrm{P}_{\mathrm{o}}\right)$
= 2P0 − Pt
For a first order reaction,
$k=\frac{2.303}{t} \log \frac{\mathrm{P}_{0}}{\mathrm{P}_{0}-p}$
$=\frac{2.303}{t} \log \frac{\mathrm{P}_{0}}{2 \mathrm{P}_{0}-\mathrm{P}_{t}}$
When $t=360 \mathrm{~s}, k=\frac{2.303}{360 \mathrm{~s}} \log \frac{35.0}{2 \times 35.0-54.0}$
= 2.175 × 10−3 s−1
When $t=720 \mathrm{~s}, k=\frac{2.303}{720 \mathrm{~s}} \log \frac{35.0}{2 \times 35.0-63.0}$
= 2.235 × 10−3 s−1
Hence, the average value of rate constant is
$k=\frac{\left(2.175 \times 10^{-3}\right)+\left(2.235 \times 10^{-3}\right)}{2} \mathrm{~s}^{-1}$
= 2.21 × 10−3 s−1
Note: There is a slight variation in this answer and the one given in the NCERT textbook.
