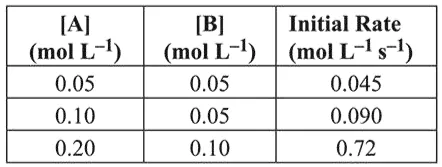
For the reaction

$2 \mathrm{~A}+\mathrm{B} \longrightarrow \mathrm{C}$

Rate $=k[\mathrm{~A}]^{x}[\mathrm{~B}\rangle^{y}$

Exp-1, $0.045=k[0.05]^{x}[0.05]^{y}$        ...(i)

$\operatorname{Exp}-2,0.090=k[0.1]^{x}[0.05]^{y}$     ...(ii)

$\boldsymbol{\operatorname { Exp }}-\mathbf{3}, 0.72=k[0.2]^{x}[0.1\}^{y}$ (iii)

Divide equation (i) by equation (ii)

$\frac{0.045}{0.090}=\left(\frac{1}{2}\right)^{x} \Rightarrow x=1$

Divide equation (i) by equation (iii)

$\frac{0.045}{0.72}=\left(\frac{0.05}{0.1}\right)^{y}\left(\frac{0.05}{0.2}\right)^{1}$

$\frac{0.045}{0.72} \times \frac{0.2}{0.05}=\left(\frac{0.05}{0.1}\right)^{y}$

$\left(\frac{1}{2}\right)^{2}=\left(\frac{1}{2}\right)^{y} \Rightarrow y=2$

Rate law $=k\lceil\mathrm{~A}\rceil^{1}[\mathrm{~B}]^{2}$