Form the differential equation of the family of circles in the first quadrant which touch the coordinate axes.

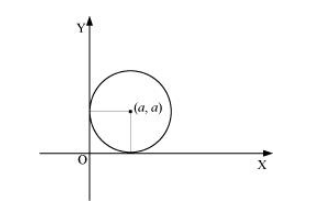
The equation of a circle in the first quadrant with centre (a, a) and radius (a) which touches the coordinate axes is:

$(x-a)^{2}+(y-a)^{2}=a^{2}$                     ...(1)

Differentiating equation (1) with respect to x, we get:

$2(x-a)+2(y-a) \frac{d y}{d x}=0$

$\Rightarrow(x-a)+(y-a) y^{\prime}=0$

$\Rightarrow x-a+y y^{\prime}-a y^{\prime}=0$

$\Rightarrow x+y y^{\prime}-a\left(1+y^{\prime}\right)=0$

$\Rightarrow a=\frac{x+y y^{\prime}}{1+y^{\prime}}$

Substituting the value of a in equation (1), we get:

$\left[x-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}+\left[y-\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)\right]^{2}=\left(\frac{x+y y^{\prime}}{1+y^{\prime}}\right)^{2}$

$\Rightarrow\left[\frac{(x-y) y^{\prime}}{\left(1+y^{\prime}\right)}\right]^{2}+\left[\frac{y-x}{1+y^{\prime}}\right]^{2}=\left[\frac{x+y y^{\prime}}{1+y^{\prime}}\right]^{2}$

$\Rightarrow(x-y)^{2} \cdot y^{\prime 2}+(x-y)^{2}=\left(x+y y^{\prime}\right)^{2}$

$\Rightarrow(x-y)^{2}\left[1+\left(y^{\prime}\right)^{2}\right]=\left(x+y y^{\prime}\right)^{2}$

Hence, the required differential equation of the family of circles is $(x-y)^{2}\left[1+\left(y^{\prime}\right)^{2}\right]=\left(x+y y^{\prime}\right)^{2} .$