Four cows are tethered at the four corners of a square field of side 50 m such that the each can graze the maximum unshared area.

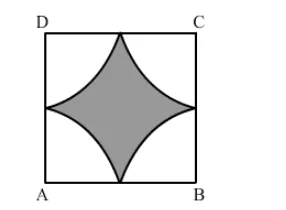
Let r be the radius of the circle.
Thus, we have:

$r=\frac{50}{2} \mathrm{~m}$

$=25 \mathrm{~m}$

Area left ungrazed $=$ (Area of the square) $-4$ (Area of the sector where $r=25 \mathrm{~m}$ and $\theta=90^{\circ}$ )

$=\left|(50 \times 50)-4\left(3.14 \times 25 \times 25 \times \frac{90}{360}\right)\right| \mathrm{m}^{2}$

$=\left|2500-\left(4 \times \frac{1962.5}{4}\right)\right| \mathrm{m}^{2}$

$=(2500-1962.5) \mathrm{m}^{2}$

$=537.5 \mathrm{~m}^{2}$