From each of the two opposite corners of a square of side 8 cm,

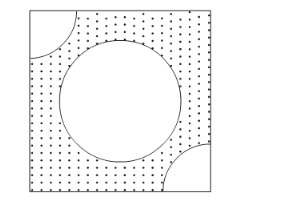
It is given that a circle of radius 4.2 cm and two quadrants of radius 1.4 cm are cut from a square of side 8 cm.

Let the side of square be a. Then,

Area of square $=a^{2}$

$=8 \times 8$

$=64 \mathrm{~cm}^{2}$

Since the radius of circle is 4.2 cm. So, 

Area of circle $=\pi \mathrm{r}^{2}$

$=\frac{22}{7} \times 4.2 \times 4.2$

$=55.44 \mathrm{~cm}^{2}$

Now area of quadrant of circle of radius 1.4 cm is,

Area of quadrant $=\frac{1}{4} \pi r^{2}$

$=\frac{1}{4} \times \frac{22}{7} \times 1.4 \times 1.4$

$=1.54 \mathrm{~cm}^{2}$

Area of shaded region $=$ Area of square - Area of circle $-2 \times$ Area of quadrant

$=64-55.44-2 \times 1.54$

$=5.48 \mathrm{~cm}^{2}$