If A(–7, 5), B(–6, –7), C(–3, –8) and D(2, 3) are the vertices of a quadrilateral

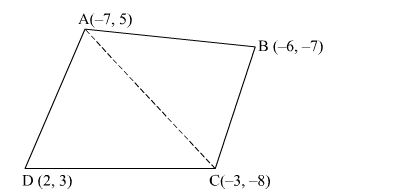
Consider the figure.

Construction: Produce $A C$ by joining points $A$ to $C$ to form two triangles, $\Delta A B C$ and $\Delta A D C$.

In $\Delta \mathrm{ABC}$,

$x_{1}=-7, x_{2}=-6$ and $x_{3}=-3 ; y_{1}=5, y_{2}=-7$ and $y_{3}=-8$

We know that,

$\operatorname{ar}(\Delta \mathrm{ABC})=\left|\frac{1}{2}\left\{\left(x_{1}\right)\left(y_{2}-y_{3}\right)+\left(x_{2}\right)\left(y_{3}-y_{1}\right)+\left(x_{3}\right)\left(y_{1}-y_{2}\right)\right\}\right|$

$\Rightarrow a r(\Delta \mathrm{ABC})=\left|\frac{1}{2}\{(-7)(-7+8)+(-6)(-8-5)+(-3)(5+7)\}\right|$

$\Rightarrow a r(\Delta \mathrm{ABC})=\left|\frac{1}{2}\{(-7)(1)+(-6)(-13)+(-3)(12)\}\right|$

$\Rightarrow a r(\Delta \mathrm{ABC})=\left|\frac{1}{2}\{(-7)+78+(-36)\}\right|$

$\Rightarrow a r(\Delta \mathrm{ABC})=\left|\frac{1}{2}\{35\}\right|$

$\Rightarrow a r(\Delta \mathrm{ABC})=\frac{35}{2}$ sq. units

Similarly, in $\triangle \mathrm{ADC}$,

$x_{1}=-7, x_{2}=2, x_{3}=-3, y_{1}=5, y_{2}=3$ and $y_{3}=-8$

$\Rightarrow \operatorname{ar}(\Delta \mathrm{ADC})=\left|\frac{1}{2}\{(-7)(3+8)+(2)(-8-5)+(-3)(5-3)\}\right|$

$\Rightarrow \operatorname{ar}(\Delta \mathrm{ADC})=\left|\frac{1}{2}\{(-7)(11)+(2)(-13)+(-3)(2)\}\right|$

$\Rightarrow \operatorname{ar}(\Delta \mathrm{ADC})=\left|\frac{1}{2}\{(-77)-26-6\}\right|$

$\Rightarrow \operatorname{ar}(\Delta \mathrm{ADC})=\left|\frac{1}{2}\{-109\}\right|$

$\Rightarrow \operatorname{ar}(\Delta \mathrm{ADC})=\frac{109}{2}$ sq. units

Now, $\operatorname{ar}($ quad. $\mathrm{ABCD})=\operatorname{ar}(\Delta \mathrm{ABC})+\operatorname{ar}(\Delta \mathrm{ADC})$

$\operatorname{ar}($ quad. $\mathrm{ABCD})=\frac{35}{2}+\frac{109}{2}=\frac{144}{2}=72$

Therefore, area of quadrilateral ABCD is 72 sq. units

Disclaimer: The answer thus calculated does not match with the answer given in the book.