If (a, b, c) is the image of the point

$\frac{x+1}{2}=\frac{y-3}{-2}=\frac{z}{-1}=\lambda$

Any point on line $=Q(2 \lambda-1,-2 \lambda+3,-\lambda)$

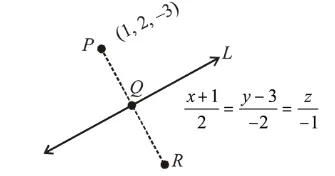
$\therefore$ D.r. of $P Q=[2 \lambda-2,-2 \lambda+1,-\lambda+3]$

D.r. of given line $=[2,-2,-1]$

$\because P Q$ is perpendicular to line $L$

$\therefore 2(2 \lambda-2)-2(-2 \lambda+1)-1(-\lambda+3)=0$

$\Rightarrow 4 \lambda-4+4 \lambda-2+\lambda-3=0$

$\Rightarrow 9 \lambda-9=0 \Rightarrow \lambda=1$

$\because Q$ is mid point of $P R=Q=(1,1,-1)$

$\therefore$ Coordinate of image $R=(1,0,1)=(a, b, c)$

$\therefore a+b+c=2$