If sin θ=12√, find all other trigonometric ratios of angle θ.

Given: $\sin \theta=\frac{1}{\sqrt{2}}$

We have to find all the trigonometric ratios.

We have the following right angle triangle.

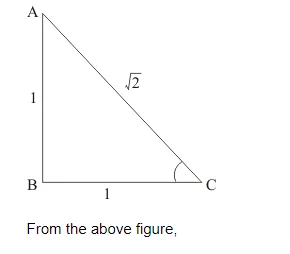
Base $=\sqrt{\text { Hypotenuse }^{2}-\text { Perpendicular }^{2}}$

$\Rightarrow B C=\sqrt{A C^{2}-A B^{2}}$

$\Rightarrow B C=\sqrt{(\sqrt{2})^{2}-1^{2}}$

$\Rightarrow B C=1$

$\cos \theta=\frac{B C}{A C}=\frac{1}{\sqrt{2}}$

$\operatorname{cosec} \theta=\frac{A C}{A B}=\frac{\sqrt{2}}{1}=\sqrt{2}$

$\sec \theta=\frac{A C}{B C}=\frac{\sqrt{2}}{1}=\sqrt{2}$

$\tan \theta=\frac{A B}{B C}=\frac{1}{1}=1$

$\cot \theta=\frac{B C}{A B}=\frac{1}{1}=1$