If sin θ=ab, find sec θ + tan θ in terms of a and b.

Given:

$\sin \theta=\frac{a}{b}$.....…… (1)

To find: $\sec \theta+\tan \theta$

Now we know, $\sin \theta$ is defined as follows

$\sin \theta=\frac{\text { Perpendicular side opposite to } \angle \theta}{\text { Hypotenuse }}$......(2)

Now by comparing (1) and (2)

We get,

Perpendicular side opposite to $\angle \theta=\mathrm{a}$

and

Hypotenuse = b

Therefore triangle representing angle $\theta$ is as shown below

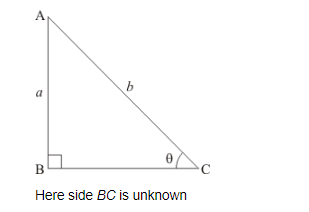
Now we find side $B C$ by applying Pythagoras theorem to right angled $\triangle A B C$

Therefore,

$A C^{2}=A B^{2}+B C^{2}$

Now by substituting the value of sides AB and AC from figure (a)

We get,

$b^{2}=a^{2}+B C^{2}$

Therefore,

$B C^{2}=b^{2}-a^{2}$

Now by taking square root on both sides

We get,

$B C=\sqrt{b^{2}-a^{2}}$

Therefore,

Base side $B C=\sqrt{b^{2}-a^{2}}$......(3)

Now we know, $\cos \theta$ is defined as follows

$\cos \theta=\frac{\text { Base side adjacent to } \angle \theta}{\text { Hypotenuse }}$

Therefore from figure (a) and equation (3)

We get,

$\cos \theta=\frac{B C}{A C}$

$=\frac{\sqrt{b^{2}-a^{2}}}{b}$

$\cos \theta=\frac{\sqrt{b^{2}-a^{2}}}{b} \cdots \cdots$(4)

Now we know, $\sec \theta=\frac{1}{\cos \theta}$

Therefore,

$\sec \theta=\frac{1}{\frac{\sqrt{b^{2}-a^{2}}}{b}}$

Therefore,

$\sec \theta=\frac{b}{\sqrt{b^{2}-a^{2}}}$.....(5)

Now we know, $\tan \theta=\frac{\sin \theta}{\cos \theta}$

Now by substituting the values from equation (1) and (3)

We get,

$\tan \theta=\frac{\frac{a}{b}}{\frac{\sqrt{b^{2}-a^{2}}}{b}}$

$=\frac{a}{b} \times \frac{b}{\sqrt{b^{2}-a^{2}}}$

=\frac{a}{\sqrt{b^{2}-a^{2}}}

Therefore,

      $\tan \theta=\frac{a}{\sqrt{b^{2}-a^{2}}}$.....(6)

Now we need to find $\sec \theta+\tan \theta$

Now by substituting the value of $\sec \theta$ and $\tan \theta$ from equation (5) and (6) respectively

We get,

$\sec \theta+\tan \theta=\frac{b}{\sqrt{b^{2}-a^{2}}}+\frac{a}{\sqrt{b^{2}-a^{2}}}$

$\sec \theta+\tan \theta=\frac{b+a}{\sqrt{b^{2}-a^{2}}} \ldots \ldots$(7)

Now we have the following formula which says

$x^{2}-y^{2}=(x+y) \times(x-y)$

Therefore by applying above formula in equation (7)

We get,

$\sec \theta+\tan \theta=\frac{b+a}{\sqrt{(b+a) \times(b-a)}}$

$=\frac{b+a}{\sqrt{(b+a)} \times \sqrt{(b-a)}}$

Now by substituting $(b+a)=\sqrt{(b+a)} \times \sqrt{(b+a)}$ in above expression

We get,

$\sec \theta+\tan \theta=\frac{\sqrt{(b+a)} \times \sqrt{(b+a)}}{\sqrt{(b+a)} \times \sqrt{(b-a)}}$

Now $\sqrt{(b+a)}$ present in the numerator as well as denominator of above expression gets cancels and we get,

$\sec \theta+\tan \theta=\frac{\sqrt{(b+a)}}{\sqrt{(b-a)}}$

Square root is present in the numerator as well as denominator of above expression

Therefore we can place both numerator as well as denominator under a common square root sign

Therefore, $\sec \theta+\tan \theta=\sqrt{\frac{b+a}{b-a}}$