If the mid-points of the sides of a quadrilateral

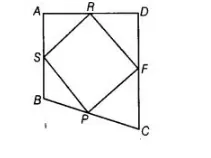
Given Let $A B C D$ is a quadrilateral and $P, F, R$ and $S$ are the mid-points of the sides $B C, C D$, $A D$ and $A B$ respectively and $P F R S$ is a parallelogram.

To prove ar (parallelogram PFRS) $=\frac{1}{2}$ ar (quadrilateral $A B C D$ )

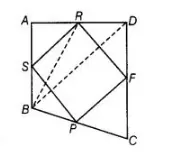
Construction Join $B D$ and $B R$.

Proof Median $B R$ divides $\triangle B D A$ into two triangles of equal area.

$\therefore \quad \operatorname{ar}(\Delta B R A)=\frac{1}{2} \operatorname{ar}(\triangle B D A)$ $\ldots$ (i)

Similarly, median RS divides $\triangle B R A$ into two triangles of equal area.

$\therefore \quad \operatorname{ar}(\Delta A S R)=\frac{1}{2} \operatorname{ar}(\Delta B R A)$ ..(ii)

From Eqs. (i) and (ii),

$\operatorname{ar}(\Delta \mathrm{ASR})=\frac{1}{4} \operatorname{ar}(\triangle B D A)$ (iii)

Similarly, $\operatorname{ar}(\Delta C F P)=\frac{1}{4} \operatorname{ar}(\Delta B C D)$ $\ldots($ iv $)$

On adding Eqs. (iii) and (iv), we get

$\operatorname{ar}(\triangle A S R)+\operatorname{ar}(\Delta C F P)=\frac{1}{4} \operatorname{ar}(\Delta B D A)$ [ $\operatorname{ar}(\Delta B D A)+\operatorname{ar}(\Delta B C D)]$

$\Rightarrow$ $\operatorname{ar}(\triangle A S R)+\operatorname{ar}(\Delta C F P)=\frac{1}{4}$ ar (quadrilateral $\left.B C D A\right)$ $\ldots(v)$

Similarly, $\operatorname{ar}(\triangle D A F)+\operatorname{ar}(\triangle B S P)=\frac{1}{4} \operatorname{ar}(q u a d r i l a t e r a l B C D A)$ $\ldots(\mathrm{vi})$

On adding Eqs. (v) and (vi), we get 

$\operatorname{ar}(\Delta \mathrm{ASR})+\operatorname{ar}(\Delta C F P)+\operatorname{ar}(\Delta D R F)+\operatorname{ar}(\Delta B S P)$

$=\frac{1}{2}$ ar (quadrilateral $B C D A$ ) $\ldots$ (vii)

But ar ( $\triangle A S R)+\operatorname{ar}(\Delta C F P)+\operatorname{ar}(\Delta D R F)+\operatorname{ar}(\Delta B S P)+\operatorname{ar}($ parallelogram PFRS $)$

$=\operatorname{ar}($ quadrilateral $B C D A)$ ...(viii)

On subtracting Eq. (vii) from Eq. (viii), we get

ar (parallelogram PFRS) $=\frac{1}{2}$ ar (quadrilateral $B C D A$ )

Hence proved.