If a $\triangle \mathrm{ABC}$ has vertices $\mathrm{A}(-1,7), \mathrm{B}(-7,1)$ and $\mathrm{C}(5,-5)$, then its orthocentre has coordinates:
Correct Option: , 3
Let orthocentre is $\mathrm{H}\left(\mathrm{x}_{0}, \mathrm{y}_{0}\right)$
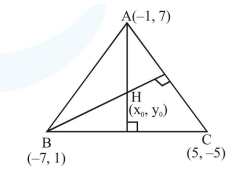
$\mathrm{m}_{\mathrm{AH}} \cdot \mathrm{m}_{\mathrm{BC}}=-1$
$\Rightarrow\left(\frac{\mathrm{y}_{0}-7}{\mathrm{x}_{0}+1}\right)\left(\frac{1+5}{-7-5}\right)=-1$
$\Rightarrow \quad 2 \mathrm{x}_{0}-\mathrm{y}_{0}+9=0$ ......(1)
and $\mathrm{m}_{\mathrm{BH}} \cdot \mathrm{m}_{\mathrm{AC}}=-1$
$\Rightarrow \quad\left(\frac{\mathrm{y}_{0}-1}{\mathrm{x}_{0}+7}\right)\left(\frac{7-(-5)}{-1-5}\right)=-1$
$\Rightarrow \quad x_{0}-2 y_{0}+9=0$ .....(2)
Solving equation (1) and (2) we get
$\left(x_{0}, y_{0}\right) \equiv(-3,3)$
