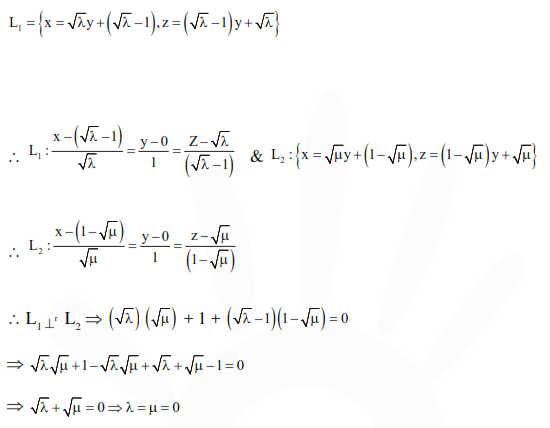If two lines L_1 and L_{2 in space, are defined by

If two lines $L_{1}$ and $L_{2}$ in space, are defined by

$\mathrm{L}_{1}=\{\mathrm{x}=\sqrt{\lambda} \mathrm{y}+(\sqrt{\lambda}-1)$

$\mathrm{z}=(\sqrt{\lambda}-1) \mathrm{y}+\sqrt{\lambda}\}$ and

$\mathrm{L}_{2}=\{\mathrm{x}=\sqrt{\mu} \mathrm{y}+(1-\sqrt{\mu})$

$z=(1-\sqrt{\mu}) y+\sqrt{\mu}\}$

then $L_{1}$ is perpendicular to $L$, for all non-negative reals $\lambda$ and $\mu$, such that :