In a rectangle ABCD, AB = 20 cm,

We have drawn the following figure

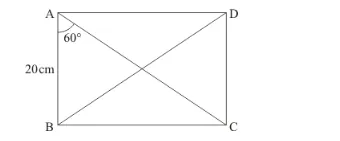
Since ABCD is a rectangle

Therefore,

$\angle A B C=\angle B C D=90^{\circ}$

Now, consider $\triangle A B C$

We know that sum of all the angles of any triangle is

Therefore,

$\angle B A C+\angle A B C+\angle A C B=180^{\circ}$.....(1)

Now by substituting the values of known angles $\angle B A C$ and $\angle A B C$ in equation (1)

We get,

$60^{\circ}+90^{\circ}+\angle A C B=180^{\circ}$

$\Rightarrow 150^{\circ}+\angle A C B=180^{\circ}$

$\Rightarrow \quad \angle A C B=180^{\circ}-150^{\circ}$

$\Rightarrow \quad \angle A C B=30^{\circ}$

Now in $\triangle A B C$

We know that,

$\cos A=\cos 60^{\circ}$

$\Rightarrow \frac{A B}{A C}=\cos 60^{\circ}$.......(2)

Now we have,

$A B=20 \mathrm{~cm}$ and $\cos 60^{\circ}=\frac{1}{2}$

Therefore by substituting above values in equation (2)

We get,

$\cos A=\cos 60^{\circ}$

$\Rightarrow \frac{20}{A C}=\frac{1}{2}$

Now by cross multiplying we get,

$20 \times 2=1 \times A C$

$\Rightarrow 40=A C$

$\Rightarrow A C=40$

Therefore,

$A C=40 \mathrm{~cm}$....(3)

Now in $\triangle A B C$

We know that,

$\sin A=\sin 60^{\circ}$

$\Rightarrow \frac{B C}{A C}=\sin 60^{\circ}$....(4)

Now we have from equation (3),

$A C=40 \mathrm{~cm}$ and $\sin 60^{\circ}=\frac{\sqrt{3}}{2}$

Therefore by substituting above values in equation (4)

We get,

$\sin A=\sin 60^{\circ}$

$\Rightarrow \frac{B C}{40}=\frac{\sqrt{3}}{2}$

Now by cross multiplying we get,

$B C \times 2=\sqrt{3} \times 40$

$\Rightarrow B C=\frac{\sqrt{3} \times 40}{2}$

$\Rightarrow B C=20 \sqrt{3}$

Therefore,

$B C=20 \sqrt{3} \mathrm{~m}$....(5)

Since ABCD is a rectangle

Therefore,

$A B=C D=20 \mathrm{~cm} \ldots .(6)$

And

$B C=A D=20 \sqrt{3} \mathrm{~cm} \ldots \ldots(7)$

Now in $\triangle B C D$

We know that,

$\tan B=\frac{C D}{B C}$

Now by substituting the values of sides from equation (6) and (7)

We get,

$\Rightarrow \tan B=\frac{20}{20 \sqrt{3}}$

$\Rightarrow \tan B=\frac{1}{\sqrt{3}}$

Since

$\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

Therefore, $\angle B=30^{\circ}$

That is in $\triangle B C D$

$\angle D B C=30^{\circ}$....(8)

Now in $\triangle B C D$

We know that,

$\cos B=\frac{B C}{B D}$

From equation (7)and (8)

$\Rightarrow \cos 30^{\circ}=\frac{20 \sqrt{3}}{B D}$

Since

$\cos 30^{\circ}=\frac{\sqrt{3}}{2}$

Therefore,

$\frac{\sqrt{3}}{2}=\frac{20 \sqrt{3}}{B D}$

Now by cross multiplying we get,

$\sqrt{3} \times B D=20 \sqrt{3} \times 2$

$\Rightarrow \sqrt{3} \times B D=40 \sqrt{3}$

$\Rightarrow \quad B D=\frac{40 \sqrt{3}}{\sqrt{3}}$

$\Rightarrow \quad B D=40$

Therefore,

$B D=40 \mathrm{~cm} \quad \ldots . .(9)$

Hence from equation (3), (5) and (9)

$A C=40 \mathrm{~cm}, B C=20 \sqrt{3} \mathrm{~cm}, B D=40 \mathrm{~cm}$