In a rhombus ABCD show that diagonal AC bisects ∠A as well as

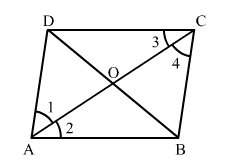
Given: A rhombus ABCD.
 
To prove: Diagonal AC bisects ∠A as well as ∠C and diagonal BD bisects ∠B as well as ∠D.
 
Proof:

In $\Delta A B C$,

$A B=B C$    (Sides of rhombus are equal.)

$\angle 4=\angle 2$    (Angles opposite to equal sides are equal.)     ...(1)

Now,

$A D \| B C$   (Opposite sides of rhombus are parallel.)

">AC is transversal.

So, $\angle 1=\angle 4$     (Alternate interior angles)          ...(2)

From (1) and (2), we get

$\angle 1=\angle 2$

Thus, $A C$ bisects $\angle A$.

Similarly,

Since, $A B \| D C$ and $A C$ is transversal.

So, $\angle 2=\angle 3 \quad$ (Alternate interior angles)

From (1) and (3), we get

$\angle 4=\angle 3$

Thus, $A C$ bisects $\angle C$.

Hence, $A C$ bisects $\angle C$ and $\angle A$

In $\Delta D A B$

$A D=A B$    (Sides of rhombus are equal.)

$\angle A D B=\angle A B D$   (Angles opposite to equal sides are equal.)     ...(4)

Now,

$D C \| A B$     (Opposite sides of rhombus are parallel.)

">BD is transversal.

So, $\angle C D B=\angle D B A$       (Alternate interior angles)          ...(5)

From (4) and (5), we get

$\angle A D B=\angle C D B$

Thus, $D B$ bisects $\angle D$.

Similarly,

Since, $A D \| B C$ and $B D$ is transversal.

So, $\angle C B D=\angle A D B \quad$ (Alternate interior angles) (6)

From (4) and (6), we get

$\angle C B D=\angle A B D$

Thus, BD bisects ∠B.

Hence, $B D$ bisects $\angle D$ and $\angle B$.