In a triangle ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q.

Let ∠ABD = 2x and ∠ACE = 2y

∠ABC = 180° − 2x [Linera pair]

∠ACB = 180° − 2y [Linera pair]

∠A + ∠ABC + ∠ACB = 180° [Sum of all angles of a triangle]

⇒ ∠A + 180° − 2x + 180° − 2y = 180°

⇒ −∠A + 2x + 2y = 180°

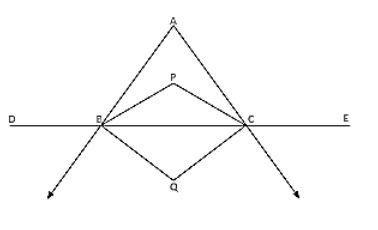
$\Rightarrow \mathrm{x}+\mathrm{y}=90^{\circ}+\frac{1}{2} \angle \mathrm{A}$

Now in ΔBQC

x + y + ∠BQC = 180° [Sum of all angles of a triangle]

$\Rightarrow 90^{\circ}+\frac{1}{2} \angle \mathrm{A}+\angle \mathrm{BQC}=180^{\circ}$

$\Rightarrow \angle B Q C=90^{\circ}-\frac{1}{2} \angle A \ldots$

and we know that $\angle B P C=90^{\circ}+\frac{1}{2} \angle A \ldots$ (ii)

Adding (i) and (ii) we get ∠BPC + ∠BQC = 180°

Hence proved.