Question:
In figure, ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60°. Compute ∠CDB, and ∠ADB.
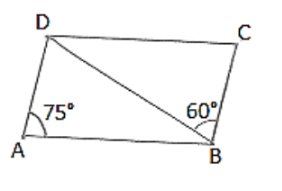
Solution:
To find ∠CDB and ∠ADB
∠CBD = ∠ABD = 60° [Alternate interior angle. AD∥ BC and BD is the transversal]
In ∠BDC
∠CBD + ∠C + ∠CDB = 180° [Angle sum property]
⇒ 60° + 75° + ∠CDB = 180°
⇒ ∠CDB = 180° − (60° + 75°)
⇒ ∠CDB = 45°
Hence, ∠CDB = 45°, ∠ADB = 60°
