In ∆PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm.

We are given the following information in the form of triangle

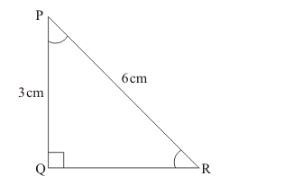
To find: $\angle P$ and $\angle R$

Now, in $\triangle P Q R$

$\cos P=\frac{P Q}{P R}$

$\cos P=\frac{3}{6}$…… (1)

$=\frac{1}{2}$

Now we know that

$\cos 60^{\circ}=\frac{1}{2}$...(2)

Now by comparing equation (1) and (2)

We get,

$\angle P=60^{\circ} \ldots \ldots(3)$

Now we have

$\sin P=\frac{Q R}{P R}$

$\sin 60^{\circ}=\frac{Q R}{6}$

Now we know that

$\sin 60^{\circ}=\frac{\sqrt{3}}{2}$

Therefore,

$\frac{\sqrt{3}}{2}=\frac{Q R}{6}$

Now by cross multiplying

We get,

$6 \times \sqrt{3}=2 \times Q R$

$\Rightarrow 6 \sqrt{3}=2 Q R$

$\Rightarrow Q R=\frac{6 \sqrt{3}}{2}$

$\Rightarrow Q R=3 \sqrt{3}$

Therefore,

$Q R=3 \sqrt{3} \mathrm{~cm}$....(4)

Now we know that

$\cos R=\frac{Q R}{P R}$

$\cos R=\frac{3 \sqrt{3}}{6}$

$\Rightarrow \cos R=\frac{\sqrt{3}}{2}$.....(5)

Now we know,

$\cos 30^{\circ}=\frac{\sqrt{3}}{2} \ldots \ldots$(6)

Now by comparing equation (5) and (6)

We get,

$\angle R=30^{\circ} \ldots \ldots(7)$

Hence from equation (3) and (7)

$\angle P=60^{\circ}$ and $\angle R=30^{\circ}$