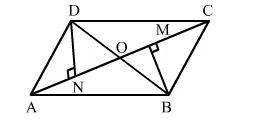
In the adjoining figure, BM ⊥ AC and DN ⊥ AC. If BM = DN,

Given: A quadrilateral ABCD, in which BM ​⊥ AC and DN ⊥ AC and BM = DN.
To prove: AC bisects BD; or DO = BO

Proof:
Let AC and BD intersect at O.
Now, in ∆OND and ∆OMB, we have:
∠OND = ∠OMB                 (90o each)
∠DON = ∠ BOM                  (Vertically opposite angles)
Also, DN = BM                         (Given)
i.e., ∆OND ≅ ∆OMB             (AAS congurence rule)
∴ OD = OB                          (CPCT)
​Hence, AC bisects BD.