In the given figure, given that ∆ABC ∼ ∆PQR and quad ABCD ∼ quad PQRS. Determine the value of x, y, z in each case.

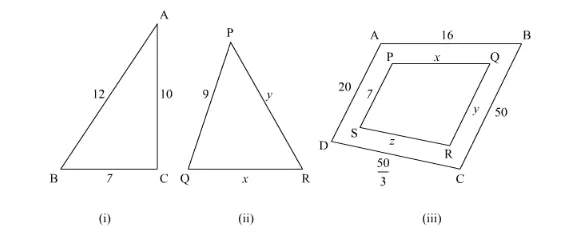
(i) We have, $\triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$

So the ratio of the sides of the triangles will be proportional to each other.

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}$

Therefore put the values of the known terms in the above equation to get,

$\frac{12}{9}=\frac{7}{x}=\frac{10}{y}$

On solving these simultaneous equations, we get

$x=\frac{21}{4}$

$y=\frac{30}{4}$

(ii) We have, $\square \mathrm{ABCD} \sim \mathrm{PQRS}$

So the ratio of the sides of the quadrilaterals will be proportional to each other.

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CD}}{\mathrm{RS}}=\frac{\mathrm{DA}}{\mathrm{SP}}$

Therefore put the values of the known terms in the above equation to get,

$\frac{20}{7}=\frac{16}{x}=\frac{50}{y}=\frac{50}{3 z}$

On solving these simultaneous equations, we get

$x=\frac{28}{5}$

$y=\frac{35}{2}$

$z=\frac{35}{6}$