Question:
In the given figure, O is the centre of a circle. Then, ∠OAB = ?
(a) 50°
(b) 60°
(c) 55°
(d) 65°
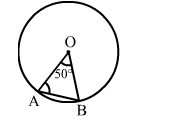
Solution:
(d) 65°
We have:
OA = OB (Radii of a circle)
Let ∠ OAB = ∠ OBA = x°
In Δ OAB, we have:
x° + x° + 50° = 180° (Angle sum property of a triangle)
⇒ 2x° = (180° - 50°) = 130°
$\Rightarrow x=\left(\frac{130}{2}\right)^{\circ}=65^{\circ}$
Hence, ∠OAB = 65°
