Question:
In the given figure, PQ and AB are respectively the arcs of two concentric circles of radii 7 cm and 3.5 cm with centre O. If ∠POQ = 30°, find the area of the shaded region.
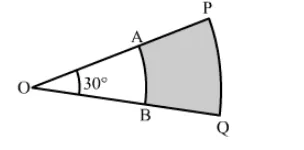
Solution:
Area of the shaded portion = Area of sector OPQ − Area of sector OAB
$=\frac{30^{\circ}}{360^{\circ}} \times \pi(7)^{2}-\frac{30^{\circ}}{360^{\circ}} \times \pi(3.5)^{2}$
$=\frac{22}{7} \times \frac{1}{12}\left[(7)^{2}-(3.5)^{2}\right]$
$=\frac{22}{7} \times \frac{1}{12}\left[(7)^{2}-\left(\frac{7}{2}\right)^{2}\right]$
$=\frac{22}{7} \times \frac{1}{12} \times \frac{147}{4}$
$=\frac{77}{8} \mathrm{~cm}^{2}$
Hence, the area of the shaded portion is $\frac{77}{8} \mathrm{~cm}^{2}$.
