In the given figure, PQ is a diameter of a circle with centre O.

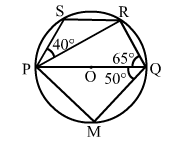
Here, PQ is the diameter and the angle in a semicircle is a right angle.
i.e., ∠PRQ = 90°
In ΔPRQ, we have:
∠QPR + ∠PRQ + ∠PQR = 180°   (Angle sum property of a triangle)
⇒ ∠QPR + 90° + 65° = 180°
 ⇒∠QPR = (180° – 155°) = 25°

In ΔPQM, PQ is the diameter.
∴∠PMQ = 90°
In ΔPQM, we have:
∠QPM + ∠PMQ + ∠PQM = 180° (Angle sum property of a triangle)
 ⇒∠QPM + 90° + 50° = 180°
⇒ ∠QPM = (180° – 140°) = 40°
Now, in quadrilateral PQRS, we have:
∠QPS + ∠SRQ = 180°   (Opposite angles of a cyclic quadrilateral)
⇒∠QPR + ∠RPS + ∠PRQ + ∠PRS = 180°
⇒ 25° + 40° + 90° + ∠PRS = 180°
⇒ ∠PRS = 180° – 155° = 25°
∴ ∠PRS = 25°

Thus, ∠QPR = 25°; ∠QPM = 40°; ∠PRS = 25°