Question:
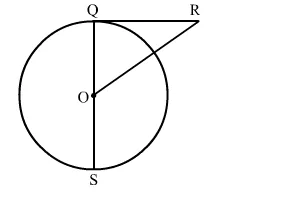
In the given figure, RQ is a tangent to the circle with centre O. If SQ = 6 cm and QR = 4 cm, then OR is equal to
(a) 2.5 cm
(b) 3 cm
(c) 5 cm
(d) 8 cm
Solution:
We know that the radius and tangent are perperpendular at their point of contact
$\mathrm{OQ}=\frac{1}{2} \mathrm{QS}=3 \mathrm{~cm}$ [∵Radius is half of diameter]
Now, in right triangle OQR
By using Pythagoras theorem, we have
OR2 = RQ2 + OQ2
= 42 + 32
= 16 + 9
= 25
∴OR2 = 25
⇒OR = 5 cm
Hence, the correct answer is option (c).
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.