In the given figure, S and T are points on the sides PQ and PR respectively of ∆PQR such that PT = 2 cm,

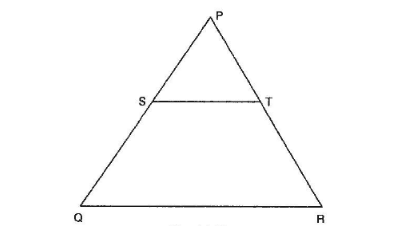
Given: In ΔPQR, S and T are the points on the sides PQ and PR respectively such that PT = 2cm, TR = 4cm and ST is parallel to QR.

To find: Ratio of areas of ΔPST and ΔPQR

In ∆PST and ∆PQR,∠PST=∠Q                    Corresponding angles∠P=∠P                         Common∴∆PST ~∆PQR           AA Similarity

Now, we know that the areas of two similar triangles are in the ratio of the squares of the corresponding sides. Therefore,

$\frac{\text { Area }(\Delta \mathrm{PST})}{\text { Area }(\Delta \mathrm{PQR})}=\frac{\mathrm{PT}^{2}}{\mathrm{PR}^{2}}$

$\frac{\text { Area }(\triangle P S T)}{\text { Area }(\triangle P Q R)}=\frac{P T^{2}}{(P T+T R)^{2}}$

$\frac{\text { Area }(\triangle \mathrm{PST})}{\text { Area }(\triangle \mathrm{PQR})}=\frac{2^{2}}{(2+4)^{2}}$

$\frac{\text { Area }(\triangle \mathrm{PST})}{\text { Area }(\triangle \mathrm{PQR})}=\frac{4}{36}=\frac{1}{9}$