In the given figure, three sectors of a circle of radius 7 cm,

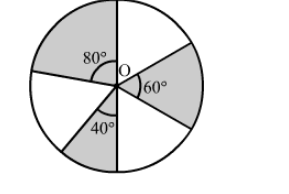
Area of the shaded region = Area of sector having central angle 60∘ + Area of sector having central angle 80∘ + Area of sector having central angle 40∘

$=\left[\frac{60^{\circ}}{360^{\circ}} \times \pi(7)^{2}\right]+\left[\frac{80^{\circ}}{360^{\circ}} \times \pi(7)^{2}\right]+\left[\frac{40^{\circ}}{360^{\circ}} \times \pi(7)^{2}\right]$

$=\pi(7)^{2}\left(\frac{60^{\circ}}{360^{\circ}}+\frac{80^{\circ}}{360^{\circ}}+\frac{40^{\circ}}{360^{\circ}}\right)$

$=\pi(7)^{2}\left(\frac{180^{\circ}}{360^{\circ}}\right)$

$=\frac{22}{7}(7)^{2}\left(\frac{1}{2}\right)$

$=77 \mathrm{~cm}^{2}$

Hence, the area of the shaded region is 77 cm2.