In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm.

Solution:

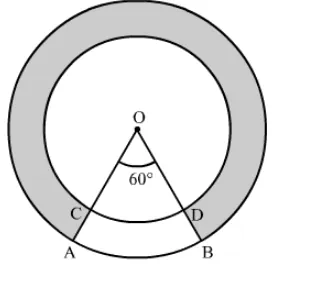
Given: Radius of the inner circle with radius OC, r = 21 cm
Radius of the inner circle with radius OA, R = 42 cm
∠AOB = 60°

Area of the circular ring

$=\pi R^{2}-\pi r^{2}$

$=\pi\left[R^{2}-r^{2}\right]$

$=\pi\left[42^{2}-21^{2}\right] \mathrm{cm}^{2}$

Area of ACDB = area of sector AOB − area of COD

$=\frac{60}{360} \times \pi \times R^{2}-\frac{60}{360} \times \pi \times r^{2}$

$=\frac{60}{360} \times \pi\left[R^{2}-r^{2}\right]$

$=\frac{60}{360} \times \pi\left[42^{2}-21^{2}\right]$

Area of shaded region = area of circular ring − area of ACDB

$=\pi\left[42^{2}-21^{2}\right]-\frac{60}{360} \pi\left[42^{2}-21^{2}\right]$

$=\pi\left[42^{2}-21^{2}\right]\left[1-\frac{60}{360}\right]$

$=\frac{22}{7}(42-21)(42+21) \times \frac{300}{360}$

$=3465 \mathrm{~cm}^{2}$