Lead spheres of diameter 6 cm are dropped into a cylindrical

Solution:

Radius of sphere $=\frac{6}{2}=3 \mathrm{~cm}$

Volume of lead sphere $=\frac{4}{3} \pi r^{3}$

$=\frac{4}{3} \pi(3)^{3}$

$=\frac{4}{3} \pi \times 27$

$=36 \pi \mathrm{cm}^{3}$

Let n be the no. of spheres are fully submerged.

Radius of cylinder beaker, $r_{1}=\frac{18}{2}$

$=9 \mathrm{~cm}$

and height of water raised = 40 cm

Clear,

The volume of raised water = n × volume of a sphere

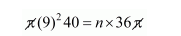
$n=\frac{81 \times 40}{36}$

$=90$

$n=90$

Hence, no. of lead sphere = 90