Question:
Let a and b respectively be the points of local maximum and local minimum of the function $f(x)=2 x^{3}-3 x^{2}-12 x$. If $A$ is the total area of the region bounded by $y=f(x)$, the $x$-axis and the lines $x=a$ and $x=b$, then $4 A$ is equal to___________
Solution:
$f^{\prime}(x)=6 x^{2}-6 x-12=6(x-2)(x+1)$
Point $=(2,-20) \&(-1,7)$
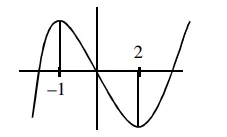
$A=\int_{-1}^{0}\left(2 x^{3}-3 x^{2}-12 x\right) d x+\int_{0}^{2}\left(12 x+3 x^{2}-2 x^{3}\right) d x$
$A=\left(\frac{x^{4}}{2}-x^{3}-6 x^{2}\right)_{-1}^{0}+\left(6 x^{2}+x^{3}-\frac{x^{4}}{2}\right)_{0}^{2}$
$4 \mathrm{~A}=114$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.