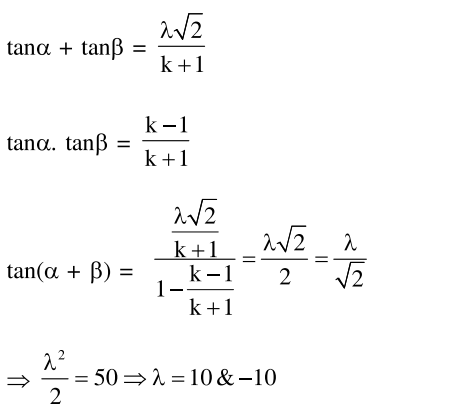Let α and β be two real roots of the equation

Let $\alpha$ and $\beta$ be two real roots of the equation $(\mathrm{k}+1) \tan ^{2} \mathrm{x}-\sqrt{2} \cdot \lambda \tan \mathrm{x}=(1-\mathrm{k})$, where $\mathrm{k}(\neq-1)$ and $\lambda$ are real numbers. If $\tan ^{2}(\alpha+\beta)=50$, then a value of $\lambda$ is ;