Question:
Minimise $Z=x+2 y$
subject to $2 x+y \geq 3, x+2 y \geq 6, x, y \geq 0$.
Solution:
The feasible region determined by the constraints, 2x + y ≥ 3, x + 2y ≥ 6, x ≥ 0, and y ≥ 0, is as follows.
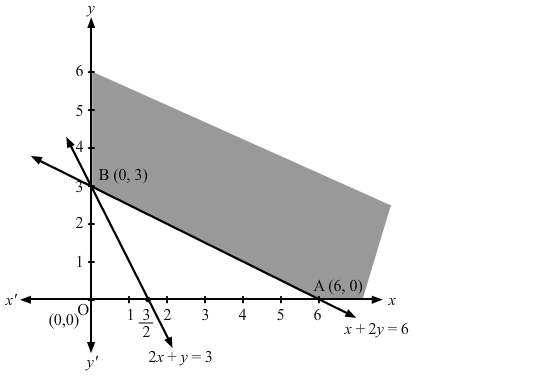
The corner points of the feasible region are A (6, 0) and B (0, 3).
The values of Z at these corner points are as follows.
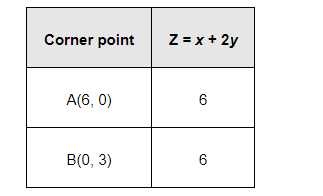
It can be seen that the value of Z at points A and B is same. If we take any other point such as (2, 2) on line x + 2y = 6, then Z = 6
Thus, the minimum value of Z occurs for more than 2 points.
Therefore, the value of Z is minimum at every point on the line, x + 2y = 6
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
