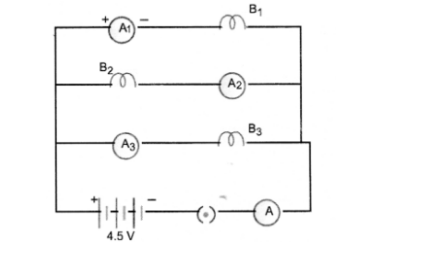
B1, B2 and B3 are three identical bulbs connected as shown in figure.

1. The glow of bulb depends upon the energy disspated per second i.e. P =V2/R.
   Since V and R of both the bulbs B2 and B3 remain the same even if bulb B, gets fused so glow of B2 and B3 remain the same.
2. Since bulbs are identical, so their resistance is equal (i.e. resistance of each bulb = R ohm).
   When all bulbs glow, net resistnace of the circuit is given by

$\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{R}}+\frac{1}{\mathrm{R}}=\frac{3}{\mathrm{R}} \quad$ or $\mathrm{R}^{\prime}=\frac{\mathrm{R}}{3}$

$\mathrm{I}=3 \mathrm{~A}, \mathrm{~V}=4.5 \mathrm{~V}$

Using $\quad V=I R^{\prime}$, we get

$4.5=3 \times \frac{\mathrm{R}}{3} \quad$ or $\quad \mathrm{R}=4.5 \Omega$

When B2 gets fused, only two bulbs B1 and B2 in parallel are in the circuit.
.’. Net resistance of the circuit is given by

$\frac{1}{R}=\frac{1}{4 \cdot 5}+\frac{1}{4 \cdot 5}=\frac{2}{4 \cdot 5}$ or $R=\frac{4 \cdot 5}{2} \Omega$

$\therefore \quad I=\frac{V}{R}=\frac{4.5 \times 2}{4.5}=2 A$

Thus, reading of ammeter $A=2 A$

Since $B_{1}$ and $B_{3}$ are in parallel and have same resistance, so $2 A$ current will be equally distributed between $B_{1}$ and $B_{3}$. Therefore, reading of ammeter $A_{1}=1 A$ Reading of ammeter $A_{3}=1 A$ Circuit containing $B_{2}$ is broken, so no current flows through this circuit. Hence reading of ammeter $A_{2}=z e r o .$

3. Power dissipated in the circuit,

P =V x I
= 4.5 x 3 = 13.5 W