Out of a group of swans, 7/2 times the square root of the

Solution:

Let the total number of swans be x.

Then, total numbers of swans are playing on the share of a pond $=\frac{7}{2} \sqrt{x}$

It is given that

$\frac{7}{2} \sqrt{x}+2=x$

Let $x=y^{2}$, then $\frac{7}{2} y+2=y^{2}$

$\frac{7 y+4}{2}=y^{2}$

$2 y^{2}=7 y+4$

$2 y^{2}-7 y-4=0$

$2 y^{2}+8 y-y-4=0$

$2 y(y+4)-1(y+4)=0$

$(y+4)(2 y-1)=0$

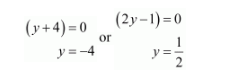
Because $y=\frac{1}{2}$ is not correct.

Thus, $y=-4$ is correct. Putting the value of $y$

$y=-4$

$\sqrt{x}=-4$

Square root both sides, we get

$(\sqrt{x})^{2}=(-4)^{2}$

$x=16$

Therefore, the total number of swans be $x=16$