Prove that the sum of all the angles of a quadrilateral is 360°.

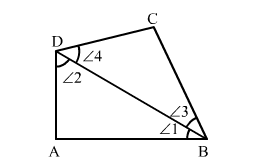
Let ABCD be a quadrilateral and ∠1, ∠2, ∠3 and ∠4  are its four angles as shown in the figure.
Join BD which divides ABCD in two triangles, ∆ABD and ∆BCD.
In ∆ABD, we have:
∠1 + ∠2 + ​∠A = 180o      ...(i)
In ​∆BCD, we have:
∠3 + ∠4 + ∠C = 180o     ...(ii)
On adding (i) and (ii), we get:

(∠1 + ∠3) + ∠A + ∠C + (∠4 + ∠2) ​= 360o  
⇒ ∠A + ∠C  + ∠B + ∠D = 360o                         [ ∵ ∠1 + ∠3 = ∠B; ∠4 + ∠2 = ∠D]
∴ ∠A + ∠C  + ∠B + ∠D = 360o