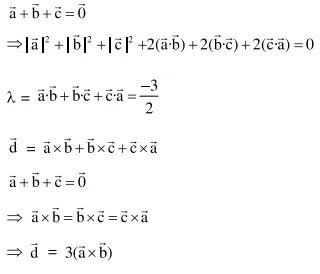Let $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}$ and $\overrightarrow{\mathrm{c}}$ be three units vectors such that $\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}=\overrightarrow{0}$. If $\lambda=\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \cdot \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \cdot \overrightarrow{\mathrm{a}} \quad$ and $\overrightarrow{\mathrm{d}}=\overrightarrow{\mathrm{a}} \times \overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{b}} \times \overrightarrow{\mathrm{c}}+\overrightarrow{\mathrm{c}} \times \overrightarrow{\mathrm{a}}$, then the ordered pair, $(\lambda, \overrightarrow{\mathrm{d}})$ is equal to:
Correct Option: 1