Refer to Example 9. How many packets of each food should be used to maximize the amount of vitamin A in the diet?

Solution:

Let the diet contain x and y packets of foods P and Q respectively. Therefore,

$x \geq 0$ and $y \geq 0$

The mathematical formulation of the given problem is as follows.

Maximize $z=6 x+3 y$

subject to the constraints,

$4 x+y \geq 80$                     (1)

$x+5 y \geq 115$                   (2)

$3 x+2 y \leq 150$                 (3)

 

$x, y \geq 0$                          (4)

The feasible region determined by the system of constraints is as follows.

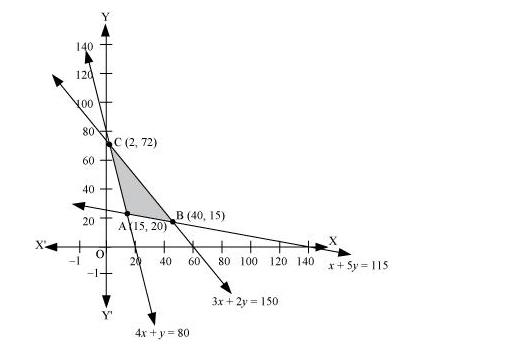
The corner points of the feasible region are A (15, 20), B (40, 15), and C (2, 72).

The values of z at these corner points are as follows.

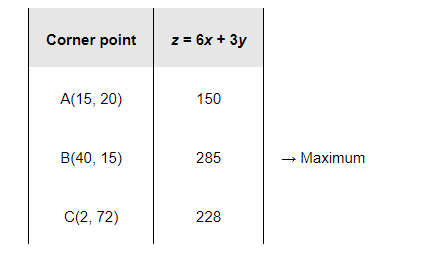
Thus, the maximum value of z is 285 at (40, 15).

Therefore, to maximize the amount of vitamin A in the diet, 40 packets of food P and 15 packets of food Q should be used. The maximum amount of vitamin A in the diet is 285 units.