Represent 10.5−−−−√ on the number line.
Learn the step-by-step geometric construction to represent √10.5 on the number line using a semicircle method with clear justification based on the Pythagorean theorem.
Represent $\sqrt{10.15}$ on the number line
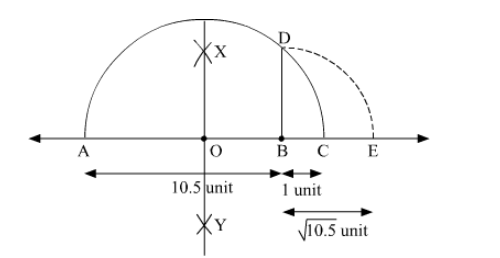
To represent $\sqrt{10.5}$ on the number line, follow the following steps of construction:
(i) Mark two points A and B on a given line such that AB = 10.5 units.
(ii) From B, mark a point C on the same given line such that BC = 1 unit.
(iii) Find the mid point of AC and mark it as O.
(iv) With O as centre and radius OC, draw a semi-circle touching the given line at points A and C.
(v) At point B, draw a line perpendicular to AC intersecting the semi-circle at point D.
(vi) With B as centre and radius BD, draw an arc intersecting the given line at point E.
Thus, let us treat the given line as the number line, with $B$ as $0, C$ as 1 , and so on, then point $E$ represents $\sqrt{10.5}$.
Justification:
Here, in semi-circle, radii $\mathrm{OA}=\mathrm{OC}=\mathrm{OD}=\frac{10.5+1}{2}=\frac{11.5}{2}=5.75$ units
And, $\mathrm{OB}=\mathrm{AB}-\mathrm{AO}=10.5-5.75=4.75$ units
In a right angled triangle OBD,
$\mathrm{BD}=\sqrt{\mathrm{OD}^{2}-\mathrm{OB}^{2}}$
$=\sqrt{5.75^{2}-4.75^{2}}$
$=\sqrt{(5.75+4.75)(5.75-4.75)} \quad\left[\mathrm{a}^{2}-\mathrm{b}^{2}=(\mathrm{a}+\mathrm{b})(\mathrm{a}-\mathrm{b})\right]$
$=\sqrt{10.5 \times 1}$
$=\sqrt{10.5}$
Frequently Asked Questions
Find answers to common questions.
What is the value of √10.5 as a decimal?
√10.5 ≈ 3.2403703... It is an irrational number, meaning its decimal expansion never terminates and never repeats. For practical purposes in constructions, you can remember it lies between 3.2 and 3.3 on the number line.
Why do we take BC = 1 unit in this construction?
Taking BC = 1 unit is essential because it makes one segment of the diameter equal to 1. When you apply the geometric mean formula, BD² = AB × BC = 10.5 × 1 = 10.5, so BD = √10.5. If BC were any other value, say 2, you would get BD = √(10.5 × 2) = √21, which is a different number entirely.
Can I use this same method to represent any irrational square root?
Yes. The geometric mean construction works for √n for any positive real value of n. Simply set AB = n and BC = 1. The perpendicular from B to the semicircle will always have length √n. This is one of the most powerful constructions in Class 9 geometry.
What theorem makes this construction valid?
The construction relies on two results: (1) the angle in a semicircle is 90° (Thales' theorem), which makes triangle OBD right-angled at D — though here we use the right angle formed at B by the perpendicular; and (2) the geometric mean relation BD² = AB × BC. Together, these guarantee BD = √(AB × BC) = √10.5.
How do I verify that my construction is correct without a calculator?
Use the bounding estimate: since 3² = 9 < 10.5 < 16 = 4², point E must lie between 3 and 4 on the number line. More precisely, 3.2² = 10.24 and 3.3² = 10.89, so E must lie between 3.2 and 3.3. Measure the distance BE in your construction — if it falls in this range, your construction is correct.