Show that the line segment which joins the midpoints

Let the trapezium ​be ABCD with E and F as the mid points of AD and BC, respectively.
Produce AD and BC to meet at P.

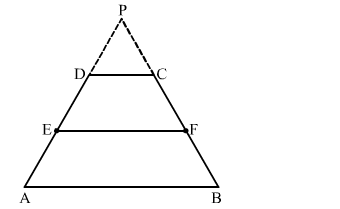
$\ln \triangle P A B, D C \| A B$

Applying Thales' theorem, we get:

$\frac{P D}{D A}=\frac{P C}{C B}$

Now, $E$ and $F$ are the midpoints of $A D$ and $B C$, respectively.

$\Rightarrow \frac{P D}{2 D E}=\frac{P C}{2 C F}$

$\Rightarrow \frac{P D}{D E}=\frac{P C}{C F}$

Applying the converse of Thales' theorem in $\Delta P E F$, we get that $D C \| E F$.

Hence, $E F \| A B$.

Thus. EF is parallel to both AB and DC.
This completes the proof.