Two small bodies of masses $2.00 \mathrm{~kg}$ and $4.00 \mathrm{~kg}$ are kept at rest at a separation of $2.0 \mathrm{~m}$. Where should a particle of mass $0.10 \mathrm{~kg}$ be placed to experience no net gravitational force from these bodies? The particle is placed at this point. What is the gravitational potential energy of the system of three particles with usual reference level?
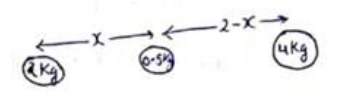
Let mass $0.5 \mathrm{~kg}$ is placed at distance $x$ from $2 \mathrm{~kg}$ between both masses. Since, particle is in equilibrium.
Force due to $2 \mathrm{~kg}=$ Force due to $4 \mathrm{~kg}$
$\frac{\mathrm{G}(2)(0.5)}{\mathrm{x}^{2}}=\frac{\mathrm{G}(4)(0.5)}{(2-\mathrm{x})^{2}}$
On solving
$x=0.83 m$
Now, gravitational potential energy
$\mathrm{U}=\frac{-\mathrm{G}(2)(4)}{2}-\frac{\mathrm{G}(2)(0.5)}{(0.83)}-\frac{\mathrm{G}(4)(0.5)}{(2-0.83)}$
$\mathrm{U}=-3.06 \times 10^{-10} \mathrm{~J}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.