Question:
If the equations $x^{2}+x+a=0$ and $x^{2}+a x+1=0, a \neq 1$, have a common root, then $a=$ ____________________
Solution:
Given:
$x^{2}+x+a=0$ and
$x^{2}+a x+1=0$ have a common root where $a \neq 1$.
Solving above 2 equations, we get
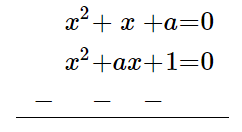
$x(1-a)+a-1=0$
i. e. $x(1-a)=+1-a$
i. e. $x=1$ $(\because a \neq 1)$ given
$\therefore a$ can be obtained form $x^{2}+x+a=0$
Since $x=1$ satisfy $x^{2}+x+a=0$
i. e. $(1)^{2}+1+a=0$
i. e. $a=-2$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.