Question:
The radius of gyration of a uniform disc about a line perpendicular to the disc equals its radius. Find the distance of the line from the centre.
Solution:
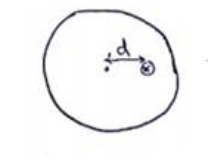
$I_{a x i s}=I_{C O M}+m d^{2}$
$m k^{2}=\frac{m r^{2}}{2}+m d^{2}$
$\Rightarrow m r^{2}=\frac{m r^{2}}{2}+m d^{2}$
$\Rightarrow d=\sqrt{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
