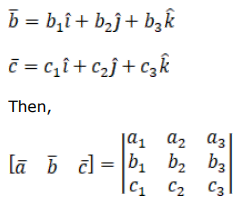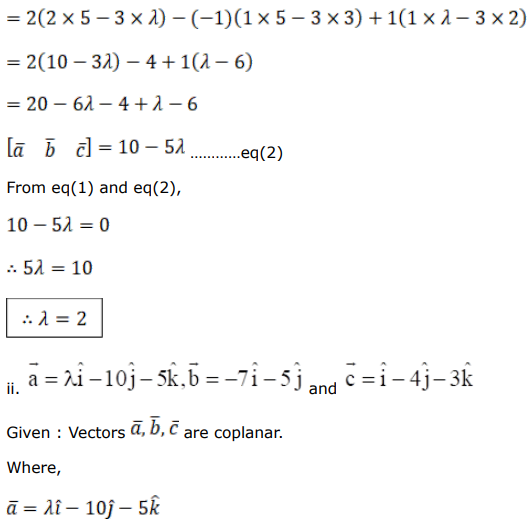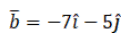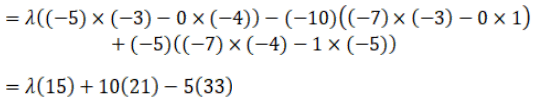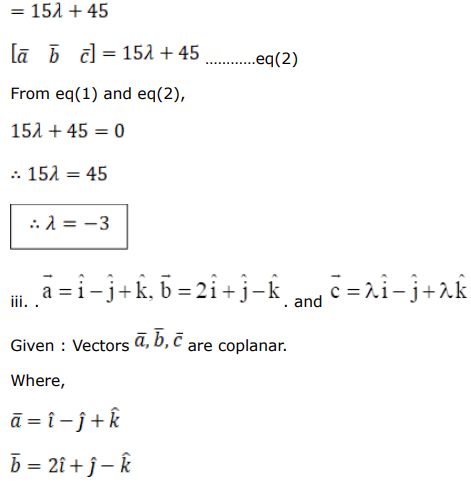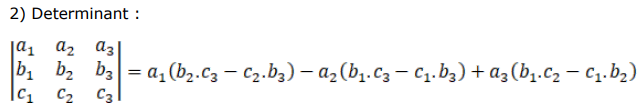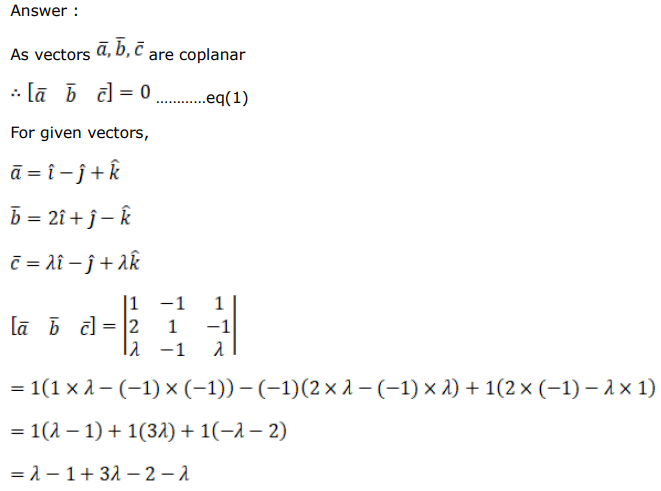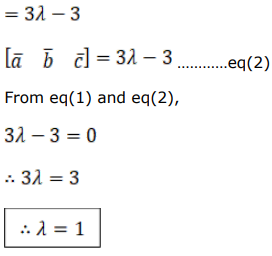Find the value of $\lambda$ for which the vectors $\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}}$ are coplanar, when
i. $\overrightarrow{\mathrm{a}}=(2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}), \overrightarrow{\mathrm{b}}=(\hat{\mathrm{i}}+2 \hat{\mathrm{j}}+3 \hat{\mathrm{k}})$ and $\overrightarrow{\mathrm{c}}=(3 \hat{\mathrm{i}}+\lambda \hat{\mathrm{j}}+5 \hat{\mathrm{k}})$
ii. $\overrightarrow{\mathrm{a}}=\lambda \hat{\mathrm{i}}-10 \hat{\mathrm{j}}-5 \hat{\mathrm{k}}, \overrightarrow{\mathrm{b}}=-7 \hat{\mathrm{i}}-5 \hat{\mathrm{j}}$ and $\overrightarrow{\mathrm{c}}=\hat{\mathrm{i}}-4 \hat{\mathrm{j}}-3 \hat{\mathrm{k}}$
iii. $\overrightarrow{\mathrm{a}}=\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}, \overrightarrow{\mathrm{b}}=2 \hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}$ and $\overrightarrow{\mathrm{c}}=\lambda \hat{\mathrm{i}}-\hat{\mathrm{j}}+\lambda \hat{\mathrm{k}}$