Question:
A bead of mass $m$ stays at point $P(a, b)$ on a wire bent in the shape of a parabola $\mathrm{y}=4 \mathrm{Cx}^{2}$ and rotating with angular speed $\omega$ (see figure). The value of $\omega$ is (neglect friction):
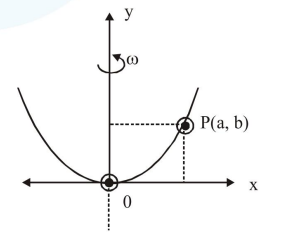
Correct Option: , 2
Solution:
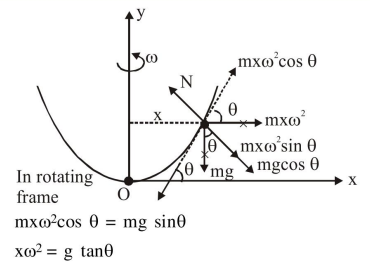
$x \omega^{2}=g \cdot \frac{d y}{d x}$
$x \omega^{2}=g .(8 c x)$
$\omega^{2}=8 \mathrm{gc}$
$\omega=2 \sqrt{2 \mathrm{gc}}$
